One of the most iconic images that shaped my career in the early days was from Madelene Rousseau’s presentation at “”Building Science Insight: ’83”…Humidity, Condensation and Ventilation in Houses…Ottawa”…”Control of Surface and Concealed Condensation” (Figure 1). Wow. Made the point of the difference between the transport of water vapor by diffusion and air flow (“leakage”). How could you not get it? I was there. I met Madelene and another legend, Rick Quirouette. More about Rick later. I was a young punk kid and they were insanely nice.
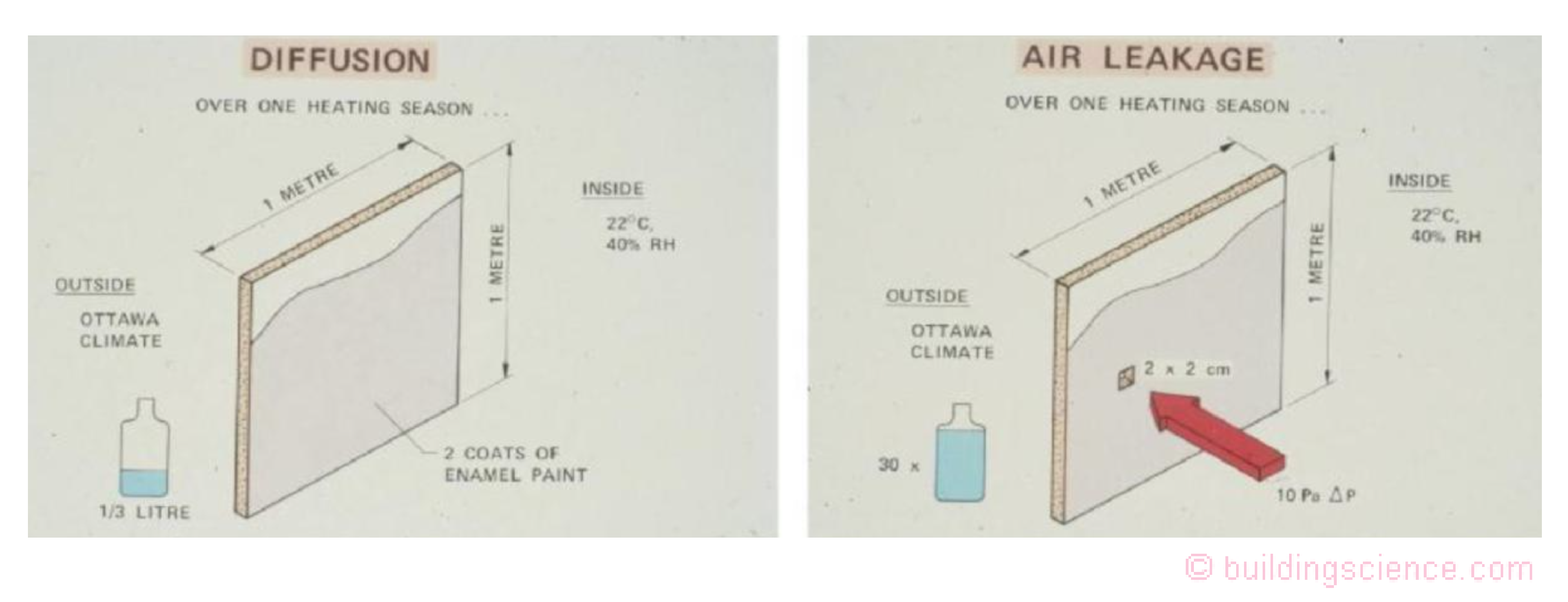
Figure 1: Madelene Rousseau: Building Science Insight: ’83”…Humidity, Condensation and Ventilation in Houses…”Control of Surface and Concealed Condensation”
When I started my career in the U.S. a year later one of my mentors…another legend…Gus Handegord, National Research Council of Canada, said “young Joseph you have to change the metric thing into real numbers for the U.S. Change a square meter into a sheet of drywall and the 2.0 cm x 2.0 cm into a square inch and move the example from Ottawa to Chicago. You better do one for Atlanta as well. So I did. I did no real calculation, just a conversion of units. I assumed 10 Pa exfiltration in Chicago and 4 Pa infiltration in Atlanta based on my field experience and chats with a bunch of rising stars in the U.S….John Tooley, Neil Moyer and Gary Nelson…. I got Figure 2 for Chicago and Figure 3 for Atlanta and started presenting them around 1985 to the weatherization folks…thank you Linda Wigington and Affordable Comfort…yup the legend Linda… It became pretty clear that air leakage was the thing…
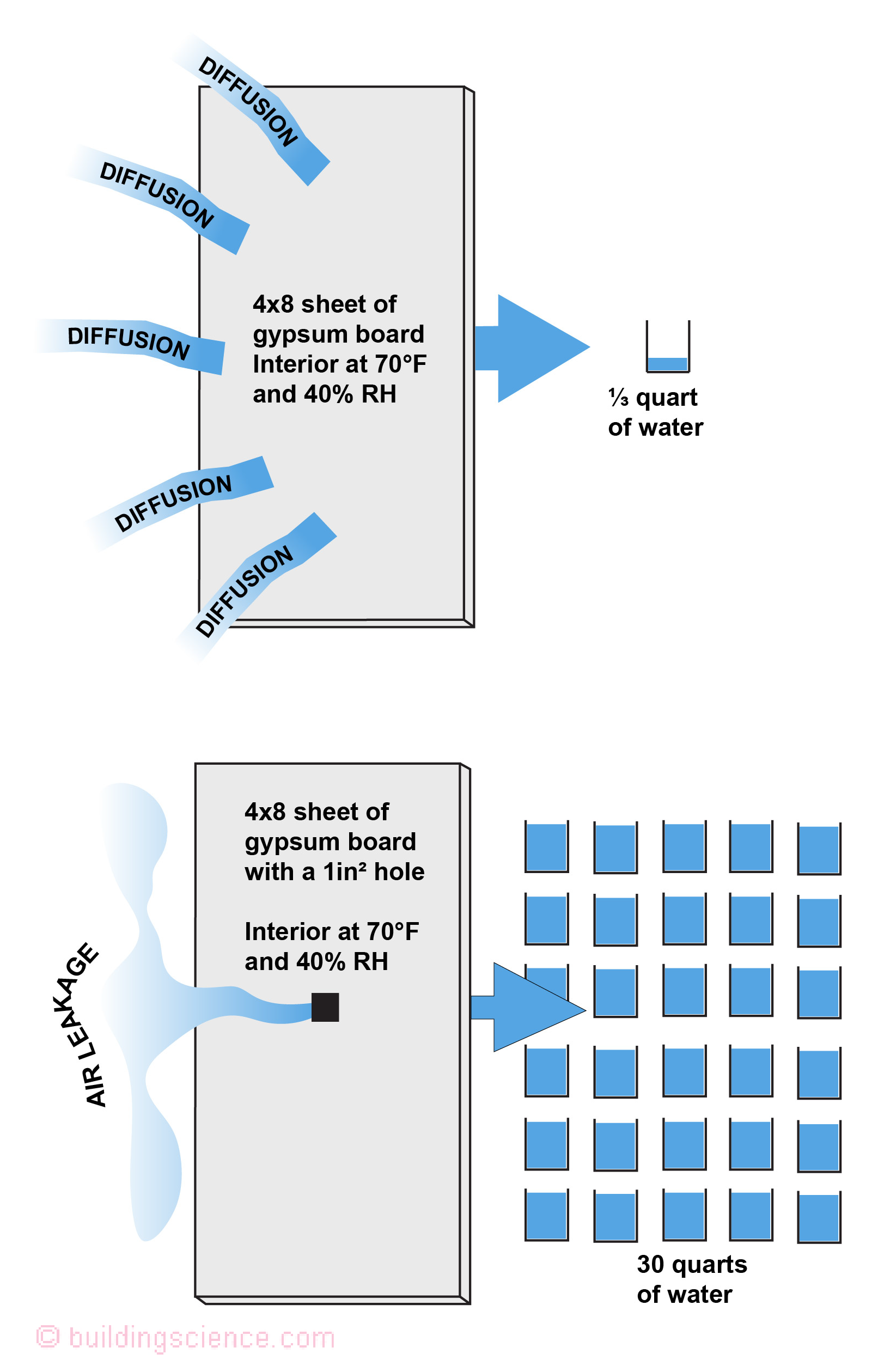
Figure 2: Air Transport vs Vapor Diffusion - In a cold climate (Chicago) the movement of water vapor over a winter from the interior to the exterior through a 1-inch square hole as a result of a 10 Pascal air pressure differential is 100 times greater than the movement of water vapor as a result of vapor diffusion through a 32-square-foot sheet of gypsum board under normal heating conditions and interior moisture levels.
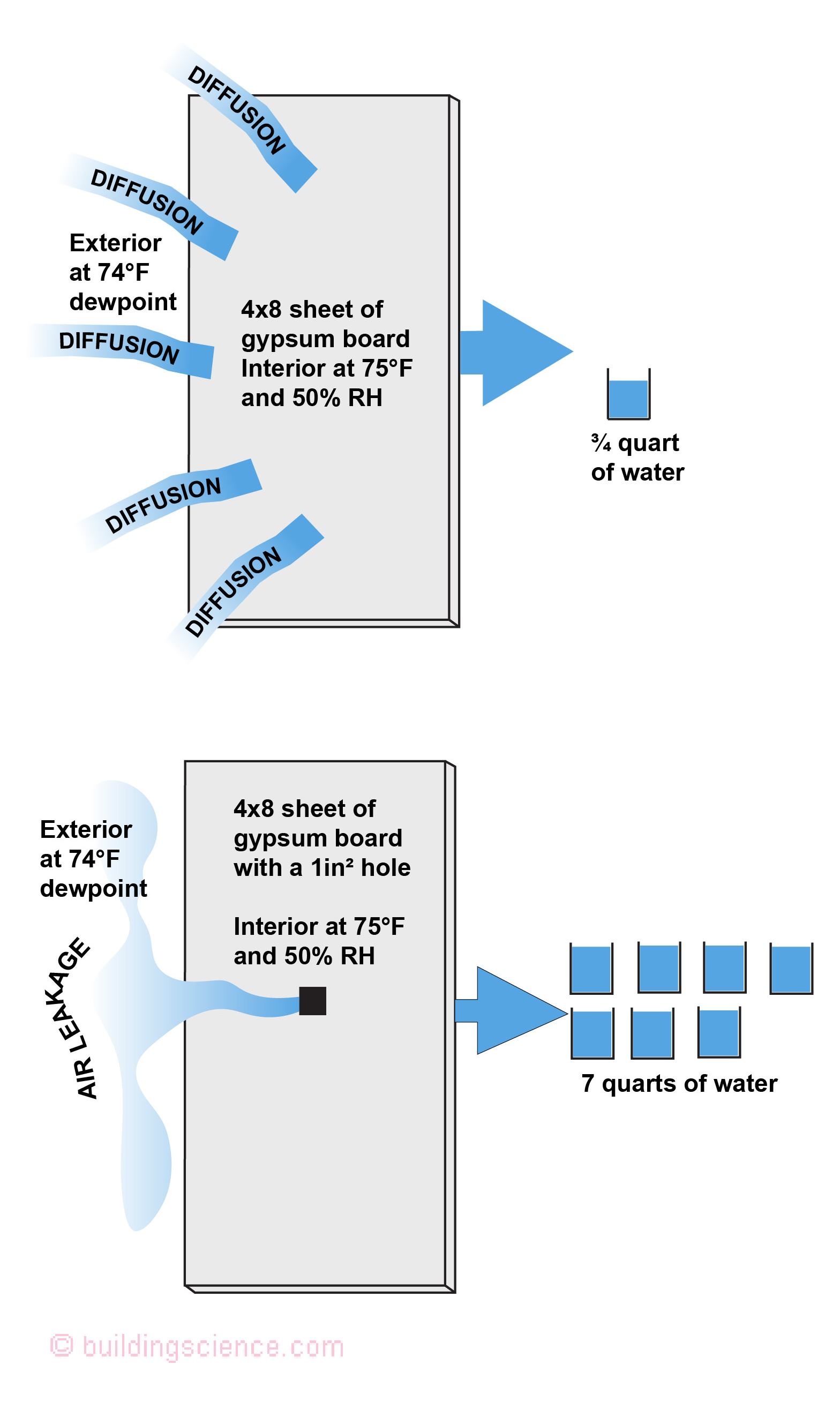
Figure 3: Air Transport vs Vapor Diffusion - In a hot-humid climate (Atlanta) the movement of water vapor over the spring, summer and fall from the exterior to the interior through a 1-inch square hole as a result of a 4 Pascal air pressure differential is 10 times greater than the movement of water vapor as a result of vapor diffusion through a 32-square foot sheet of painted gypsum board under normal cooling conditions and exterior moisture levels.
I wrote a series of books….called Builders Guides…the figures were in the Builders Guides…I wrote the first guide in 1989…they have been reprinted and updated since then…thousands of them in circulation…the latest version was 2022.
So I am working on my Doctorate in early 1990 and one of my advisors…another legend Mark Bomberg (he has two Ph.D.’s…we call him “Doctor-Doctor”)…and I are having a cup of coffee in the cafeteria at the Division of Building Research (DBR), National Research Council of Canada, Ottawa…and he starts chatting with me about how things get done in this cafeteria… I asked, how so? “Well Madeline and I were having a cup of coffee here a long time ago and we were trying to figure out the differences in magnitude between air transport of vapor and vapor transport by diffusion and Dick Solvason comes by and sits down with us.” I interject “Dick Solvason? For real? That Dick Solvason?” Dr. Bomberg starts laughing, “There was only one…yes, for sure..” According to Dr. Bomberg, Solvason says, “This is pretty easy, give me your cigarette package”. Dr. Bomberg proceeds to explain that Dr. Solvason took out his slide rule, a pencil out of his pocket protector and proceeded to do the calculation on the front and back of a “Lucky Strike” package. I burst out laughing…I understood right away…
Back in the day we engineers did not have calculators, we had slide rules (Photograph 1). With a slide rule you did not know where the decimal point ends up….you had to do an “order of magnitude” calculation. The engineering joke was that if you could not do the order of magnitude calculation on a Lucky Strike package you did not know enough to do the calculation. Why Lucky Strike? Ah, it had a big red dot on the package and you had to do the calculation around the red dot (Photograph 2). All of us engineers back in the day were known as “Lucky Strike engineers”. I was in the last engineering class at the University of Toronto that was not allowed to use a calculator…I had a big slide rule, a pocket protector and a Lucky Strike package…even though I did not smoke. Yup, right out of central casting, short sleeve white collar shirt with a pocket protector and a Lucky Strike package. You youngsters should go and look at some old photos of the NASA engineers…short sleeve white shirts, pocket protectors and a tie…
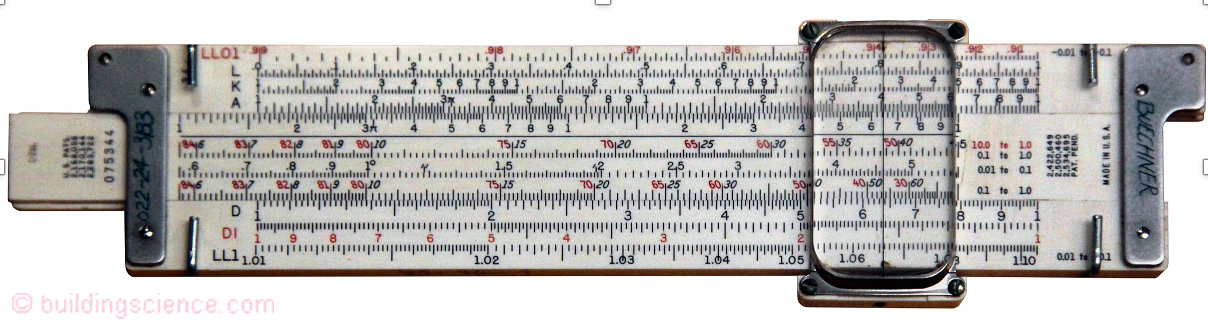
Photograph 1: Slide Rule

Photograph 2: Lucky Strike
Dr. Bomberg proceeds to explain that Madeline Rousseau points out that they can’t present the information to “normal folks” using a cigarette package…even if it is Dick Solvason’s….so she created the image that educated me and countless others…
More than 3 decades pass and I am in a cafeteria in Golden, CO…at NREL...I have just done a presentation on building science…talked about the history of the image…and one of the youngsters having coffee with me asks..”So how did the slide rule calculation hold up?” I go silent, and then commented…”Pretty sure DBR at the National Research Council of Canada did a detailed analysis. I think I know who did that work…Rick Quirouette…he wrote one of the all time classics and the calculation is in his paper: “The Difference Between A Vapor Barrier and An Air Barrier, R.L.Quirouette, BPN 54, July, 1985, National Research Council of Canada.” I used to hand out copies of Rick’s paper to all who attended my presentations in the 1980’s and 1990’s.
I get back home and re-read Rick’s paper…he has the calculation right there..the difference with Rick’s was 200 to 1 rather than Solvason’s 100 to 1. Wow. No one ever said anything. Rick is a classy guy, big time. New legends respect old legends. Rick’s calculation was in 1995. I now can’t sleep. We have amazing analysis tools available now. Why not look at what we come up with using the state of the art today…so…
Who to do the work? Easy, someone from the next generation of legends…Chris Schumacher is the one I picked. Guess what? Chris’s analysis approach is in the side bar. Bottom line. Air transport is way more than I thought and way more than the old legends thought. The new graphics are presented….Chicago is Figure 4 and Atlanta is Figure 5. Wow. Double wow. Chicago air transport of moisture gain is 95 quarts…not 30..it is 100 to 1… Atlanta air transport of moisture gain is 30 quarts not 7…it is also 100 to 1. How about the original Ottawa calculation…it should have been 80 quarts not 30….it is 250 to 1. Guess what…Rick Quirouette was 200 to 1…in 1995…remind me to buy him a stiff drink when I see him and shake his hand. All summarized in Table 1.
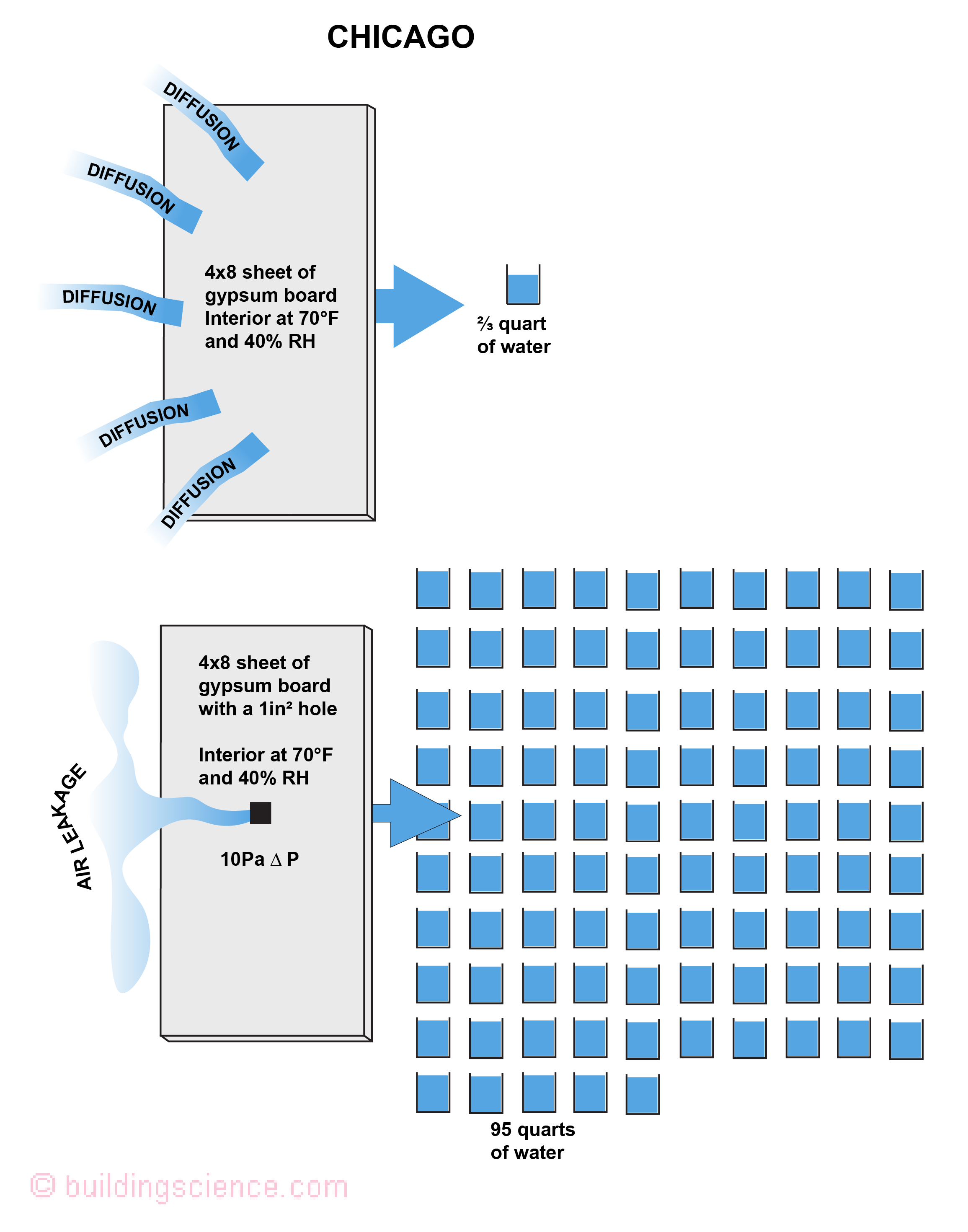
Figure 4: Air Transport vs Vapor Diffusion – Chicago - the movement of water vapor over a winter from the interior to the exterior through a 1-inch square hole as a result of a 10 Pascal air pressure differential is 200 times greater than the movement of water vapor as a result of vapor diffusion through a 32-square-foot sheet of gypsum board under normal heating conditions and interior moisture levels.
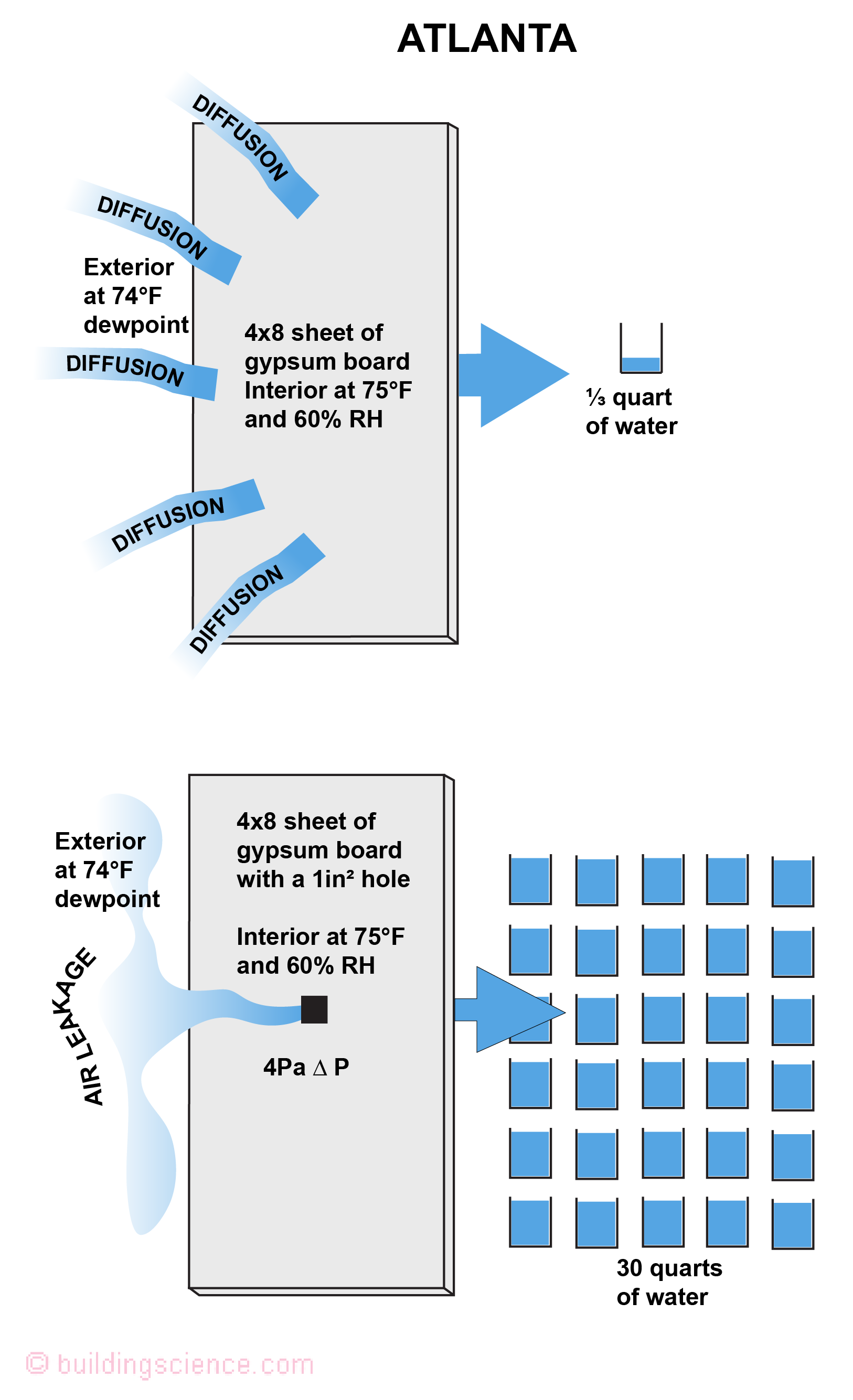
Figure 5: Air Transport vs Vapor Diffusion – Atlanta - the movement of water vapor over the spring, summer and fall from the exterior to the interior through a 1-inch square hole as a result of a 4 Pascal air pressure differential is 100 times greater than the movement of water vapor as a result of vapor diffusion through a 32-square foot sheet of painted gypsum board under normal cooling conditions and exterior moisture levels.

Table 1: Air Leakage vs Diffusion
Schumacher’s steps for reproducing Solvason’s/Rosseau’s diffusion vs air leakage calculation of ’83 (using modern calculation tools):
- Retrieve Ottawa climate data that Solvason/Rousseau et. al. would have referenced back in 1983. These can be found in the Canadian Climate Normals Volume 8, Atmospheric Pressure, Temperature and Humidity, 1951-1980 (Canadian climate normals 1951-1980 - Normales climatiques au Canada 1951-1980 v.8).
- Solvason’s/Rousseau’s text indicates the original analysis considered a five-month period over an Ottawa winter, but doesn’t indicate which months. We assume the five coldest months: Nov-Mar, a period of 151 days, and use the average outdoor drybulb temperature (-5.9C or 21.5F) and dewpoint (-10.1C or 14F) to calculate the average outdoor RH (69%) [Refer to ASHRAE HOF chapter, “Psychrometrics”]
-- First, considering Vapor Diffusion --
- Solvason/Rousseau stated the assumptions for the indoor conditions: 22C (72F) and 40% RH. Again we refer to the ASHRAE HOF “Psychrometrics” to calculate the water vapor pressure of the outdoor air: 1058 Pa (0.312 inHg), and indoor air: 258 Pa (0.076 inHg)
- Solvason/Rousseau assumed 1 m2 (10.8 sq. ft.) area of gypsum board with two coats of enamel paint. Now, referring to ASHRAE HOF chapter, “Thermal and Water Vapor Transmission Data”, we estimate the vapor permeance of the painted gypsum board is about 28.5 ng/Pa.s.m2 (0.5 US Perms).
- Referring to ASHRAE HOF chapter “Thermal and Moisture Control in Insulated Assemblies”, we calculate the total amount of vapor Diffusion = vapor Permeance of painted drywall x Area of drywall x Vapor Pressure Difference (in to out) x total time (i.e., over 151 days) = 0.30 kg or 0.32 US quarts. Note this is almost exactly the 1/3 Litre that Rousseau indicated in her diagram!
-- Now, considering Air Leakage --
- Once again referring to ASHRAE HOF “Psychrometrics”, we calculate the density of the indoor air: 1.20 kg/m3 (0.075 pcf), and the humidity ratio of the indoor air: 6.56 g/kg (45.9 grain/lb) and outdoor air: 1.59 g/kg (11.1 grain/lb)
- Rousseau’s diagram indicates that air leakage is considered through a 2 x 2 cm hole (4 cm2 or 0.62 sq. in.) and under an air pressure difference of 10 Pa. Referring to ASHRAE HOF chapter, “Ventilation and Infiltration”, we estimate the airflow rate through the hole = 0.6 x Area of hole x square root of (2 / Density x Air Pressure Difference) = 0.99 lps or 2.09 cfm.
- Now we calculate the amount of moisture gained as a result of this air leakage. Note this is less than the amount of moisture moved through the hole as there was already some moisture on the other side. The total moisture gain by air leakage = volumetric Airflow rate x Density of dry air x Difference in Humidity Ratio (in to out) x total time (i.e., over 151 days) = 77 kg or 81 US quarts. Note this is about 2.5 times the amount indicated in the Rousseau image but close to that calculated by Quirouette in his analysis of the same problem.
-- Conclusion –
- Reanalysis of the Ottawa example presented by Solvason /Rosseau suggests that Air Leakage moves approximately 256 X more moisture than Vapor Diffusion.
Schumacher’s steps were repeated for the Chicago and Atlanta figures.
